Advanced Techniques: X-Wing
Hey guys, welcome back to Sudokumania, the home of online sudoku where we provide you with free sudokus daily. Yes we do have daily sudokus and not just classic sudokus, but a whole lot of Sudoku Variants. So, first of all, apologies for the long absence. Had to take care of some pending issues.
Now that we have already covered the basic techniques, it is time to delve into some of the advanced techniques that will help us crack open some tough and very hard sudokus. It is worth remembering that these advanced techniques do not provide a solution digit ever, but they help us in eliminating options/pencil marks in given cells which in turn allow us to narrow down to a single digit in a cell. If you missed the last blog post, you can read it here at the given link. It was about Naked and Hidden Pairs.
So in today’s post we will have a look at the most common advanced technique called X- Wing. I will also place links to sudokus which use these techniques, at the end of the post for you to practice the said techniques.
X-Wing
Though it is difficult to put into words, I will try and explain it. Basically when using this technique, we look for a digit which can occur in only two columns of a row (or two rows in a specific column). Then we look for the same digit in a different row where it occurs exactly in the same two columns as earlier. I know this sounds a bit confusing, but let us take a look at the image example given below. Hopefully it will help us understand the technique better.
In the image given below, for Row 1, the number 9 can be only in R1C2 or in R1C9. Similarly for Row 9 it can be in either R9C2 or in R9C9. I have circled these 4 cells and if you were to draw lines joining the opposite ends, they would form a perfect X. Hence the name X-Wing.
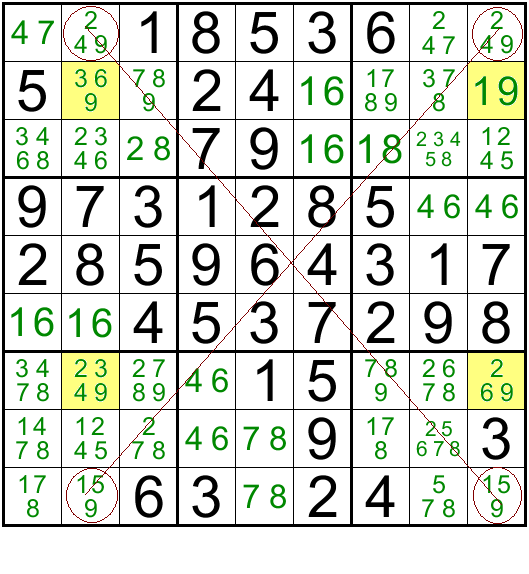
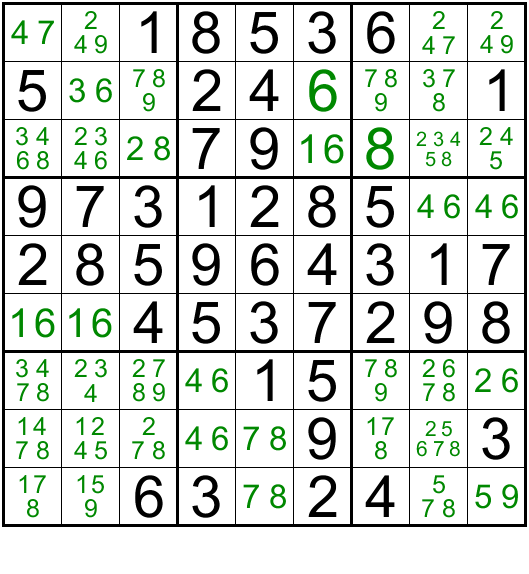
If 9 is in R1C2, then it gets eliminated from R9C2 and has to be in R9C9. Conversely, if 9 is in R1C9 then it is eliminated in R9C9 and has to be in R9C2. So the number 9 will always be on either end of one line of the X shape, and that takes care of number 9 for column 2 and Column 9. Hence for columns 2 and 9, the number 9 can be only in either Row 1 or Row 9 and nowhere else. Hence 9 as a possibility can be eliminated from the cells in these two columns. (Highlighted in yellow). This helps us eliminate 9 from R2C9 and we get a naked single 1 as the only option available for R2C9. Using this 1 we can slowly unravel the sudoku.
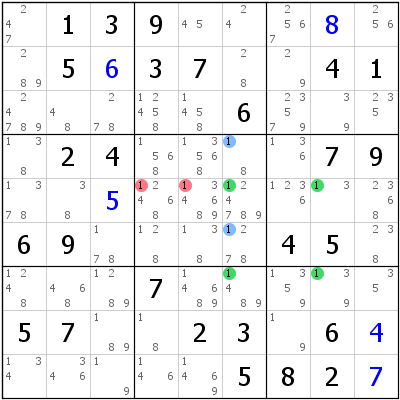
Now that we have understood the X-Wing technique, there is a variation to it which I personally find very beautiful. It is very difficult to observe. It is an extension to the X-Wing. In an X-Wing we are looking for four cells in a rectangle which contain a candidate N that exists just twice in either the two rows that form the rectangle or the two columns. Our Finned version is still a rectangle but it has extra candidates of the number in question that prevent one of the two pairs we need from existing. Let us look at the given image below. In Columns 6 and 8 if we had 1s only in the green cells then it would have been an X-Wing and we would have been able to eliminate 1s from R5 and R7. But unfortunately that is not the case so. In Column 6, we have additional 1s marked in blue. So how does this help us?
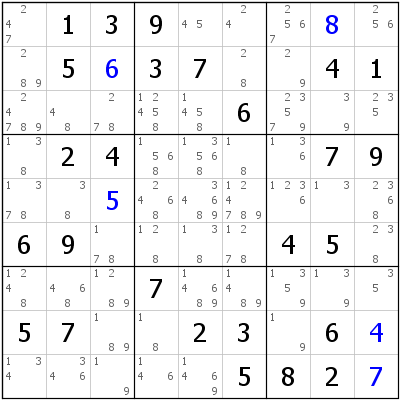
Now in C6, if 1 was in R7C6, then 1 would be placed in R5C8 thus allowing us to eliminate all ones in R5. But if 1 is not in R7C6 then it has to be in C6 in Box 5 in any of the 3 cells, which would allow us to eliminate 1s from Box 5. In either of these 2 scenarios, the common factor being cells which are either part of R5 and also Box 5. These common cells are marked in red. Hence we can safely assume that irrespective of where 1 comes in Column 6, it cannot be in R5C4 and R5C5.
Hope this was helpful to you all and do leave a comment on your feedback, suggestions or if you would like to see a post on a specific topic. So till the next time, Happy Solving :)
Practice Sudoku
Put the concepts shared in today's post to practice by trying to solve these puzzles: